- ... quality).1
- Further, hardware implementations of algorithms often yield speed increases
of approximately an order of magnitude. This algorithm may not be suited to
having a full hardware implementation (as it requires substantial amounts of
memory for reasonable resolution images), but parts of it may be suited to hardware
implementations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dimensions2
- Which also has the additional feature of being its own Fourier transform, that
is,
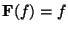 for
for
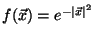 .
More generally, the Fourier transform of a Gaussian function is also a Gaussian
function (with different constants).
.
More generally, the Fourier transform of a Gaussian function is also a Gaussian
function (with different constants).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... shells3
- For the three dimensional images that we are using. Naturally if we were dealing
with two dimensional images we would expect to find thin rings.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
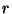 4
4
- Or at the very least, a mask-based smoothing operation as detailed in Section
2.1.1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integer)5
- Implemented by taking the first 100 terms of the infinite sum describing
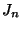 ,
and precomputing the values of
,
and precomputing the values of 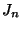 for the values of
for the values of 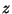 that
would be required. The sum used was
that
would be required. The sum used was
as derived in [Kreyszig, 1993, Section 5.5, page 227].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... values6
- The file format actually has an option to use (big-endian) word length pixels
(giving 65536 possible pixel values), however none of our data files used this
feature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 256)7
- This was also observed to be a natural choice, as the images produced by the
equipment have low level noise values of approximately this value where no signal
is received.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
points8
- Here, 1k = 1024, as is standard for computing applications.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time9
- Note that this is the CPU time required to do the calculations. The actual wall-clock
time taken for the program to run was substantially higher than these figures,
due to the large amounts of IO required (and often also virtual memory swapping).
The machine used to run these tests was an Intel Celeron 300Mhz (128kb CPU cache,
overclocked to 450MHz) with 128Mb RAM running Linux.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time10
- Here we are using
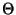 -notation (related to big-Oh notation), which
denotes the set of functions
-notation (related to big-Oh notation), which
denotes the set of functions
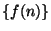 that are asymptotically
bound by
that are asymptotically
bound by 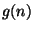
Also, in our notation
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... well11
- Compared to the exact solutions which have exponential time complexity.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
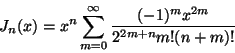
![]() .
.